CY(Carry)： 用于表示加法进算中的进位和减法运算中的借位，加法运算中有进位或减法运算中有借位则CY位置1，否则为0

OV： 表示运算过程中是否发生了溢出，若运算结果超过了8位二进制数所能表示数据的范围即有符号数-128~+127，则标志位置1。

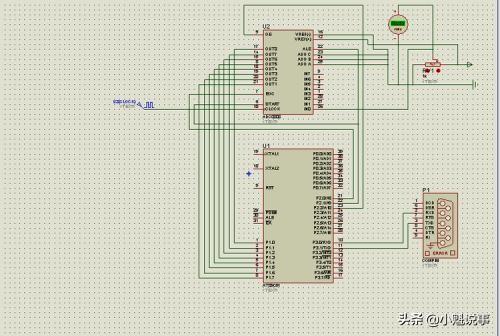
单片机中的CY与OV详细解析

对无符号数的运算，判断只需CY即可，OV无作用。

对有符号数的运算，OV位是有用的。“OV位是C6位进位与C7位进位的异或”，说法对的(对51单片机而言)，但不同的计算机说法不一

CY位是累加器的进位、借位标志。下文的叙述按16位机来举例说明，如果是8位机或其它字长，则可换一个例子，但道理相似。

对于无符号数的运算，CY位就可以表示其是否溢出。但如果是有符号数，则不能按CY标志来判断了。为此，设了另一个标志OV，其含义就是“假如是有符号数运算，是否出现了溢出”。

例如对于16位运算器，65534 + 3，(即二进制的1111111111111110 + 0000000000000011)，

本该得65537，(即二进制的10000000000000001)，但因为寄存器只有16位，最高位的那个1丢掉了(进入了CY标志)。结果寄存器中只剩下了1，(即二进制的0000000000000001)。

此时，我们可以说，16位的无符号数加法，65534+3溢出了，溢出后的答案成了1。

但是对于有符号整数，情况就不同了。有符号整数采用补码表示法。16位有符号整数不可能表示65534，此时如果机内二进制是1111111111111110，程序中认为它是-2，故：

机内的二进制的1111111111111110 + 0000000000000011，代表的是(-2) + 3。

请注意，此时的(-2)+3和上文的无符号数65534+3，在CPU的运算器硬件上完全相同，都是得到和为1，而CY标志也为1。

但是，有符号数(-2)+3=1并无溢出。故此时的CY标志不能代表它溢出了。

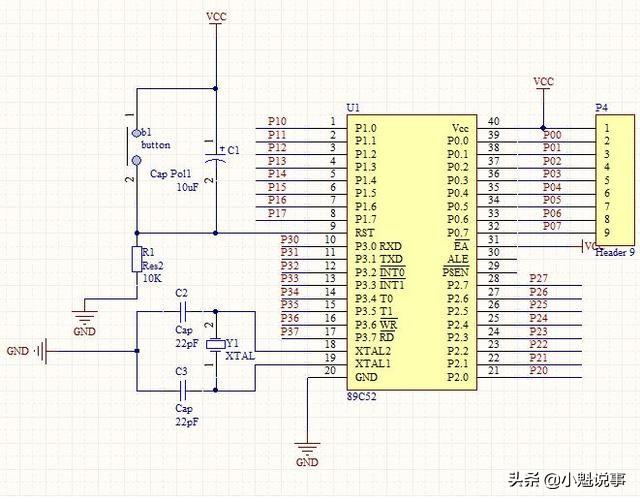
另外再举一例：

无符号数32763 + 8 = 32771，没有进位，CY标志为0。此时并不溢出。

但是，如果是有符号数32763 + 8，这就是溢出了，因为32773的二进制为1000000000000011，作为有符号数会被看成负数-32765。16位有符号数不可能表示32773的。

不管是有符号数还是无符号数，CPU的二进制运算器机器加、减操作是一样的，但其“溢出”的条件不同。

现在大多数的计算机中，如果是无符号数，都可以用CY标志来判断其是否溢出；而如果是有符号数，则需要用OV标志来判断其是否溢出。

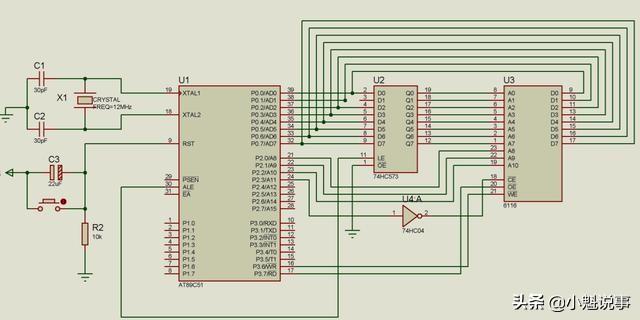
至于OV标志在逻辑上又是根据什么产生的呢？则不同的计算机上有不同的实现方法，但效果都是一样。

这里介绍一种道理比较容易懂的方法：“双符号位法”。具体是：

作加、减法前，先将两个运算数都按照有符号数的规则扩充成17位。即：符号位是0的前面添一位0，符号位是1的前面添一位1。

然后按17位的机器加、减，得出17位的结果。

如果17位结果的高两位(即双符号位)不同，就置OV标志为1，否则，OV标志为零。